Uzay yaratılmadan önce

   Evrenin internet explorer tarayıcısı gibi sanal makine olduğunu ve üzerindeki bilgilerin maddenin 

htlm  canlı organizmanın da DNA sı java kodları olduğunu kabul edersek yaşadığımız dünyanın

internetteki siber uzaydan hiç bir farkı kalmaz.

 Bilgisayarda her şey 1 ( varlık =iletişim ) 0 ( yokluk = iletişimsizlik ) olarak tanımlı büyük bir

sayıdır. Bu sayının 0 , 1 birimlik n boyutlu uzay olarak tanımlarsak her şeyin 0 noktasında yoklukta

tanımlamış oluruz. Her türlü fonksiyonu geometrik anlamı hayal olduğu ortaya çıkar.

        Zaman , mekan ve madde nedir ? Niçin üç boyutlu olarak dünyayı algılarız ?

      N ! = Permitasyon = Zaman : Diziliş ( N   den   -------->      N e Bire bir örten toplam fonksiyon sayısı )

      2ⁿ = Kombinasyon= Mekan   : Birleşim ( Pisagor üçkeni , olasılık toplamı n!/(x!*(n-x)!))

       1 ! =1 < 2 üzeri 0 =1

     2! =2 < 2*2

      3! = 6 < 2*2*2 = 8

      4! =24 > 2*2*2*2 = 16

      5! =120 > 2*2*2*2*2 =32      

     Zaman kavramını oluşturan dizilişi kontrol eden sistemdir . Dizilişte değişen birimler maddeyi , değişmeyen kısımlar boşluk kavramını ortaya çıkarır .

        3 ten büyük sayı için aynı an kavramı oluşmaz .   

      Yanı üç boyutludan fazla  uzayı algılanamaz . n! < 2ⁿ   koşulu olmak zorundadır. Zamanın içine mekan

 sığabilmesi için ! . Yoksa zaman kavramı oluşmaz geçmiş ve geleceği aynı anda algılarız. 

        Örneğin :  Bilgisayar  ekranında 10 pencere açtın 1000 siteyi inceleyeceksin . 100 ! permutasyon şeklinde bu siteleri inceleyebilirsin. ( hayalın ötesinde bir değer . )

   İç dünya  10 ! Permutasyon  ( Zaman kavramı ) > 2¹⁰. Kombinasyon  ( Mekan kavramı ) 

   Diş dünya    1000! / (1000-10)! Permutasyon > 1000!/10!/(1000-10)! kombinasyon  vardır.

 İletişim  (Küme elemaları + küme eleman dizme sistemi + küme elemanı seçme sistemi= hafıza  + algoritma + girdi ve çıktı ,  Yazılım = Ruh = İç dünya )

  İletişim kanalı  ( Küme uzayı + küme şecen sistem + küme =  bilgi kayıt ortamı + bilgi kontrol + bilgi          ,Donanım = Beden = Dış dünya  ) 

 Hız = Yol / Zaman          dalga boyu = iç  iletişim kanal sayısı  = y 

frekans =Kombinezon  /  Permutasyon =>  n! / ( ( n-x)!*x!) / n!/(n-x)! = 1/x!

L _x=v t = y ^x  / x! f ^x(0)      anlık durum değeri ( 100 veya 500 gözlem gibi )

f ^x(0)  = 0 anındaki ( şu an ) gözlem değeri 

Örneğin : 10 pencere ile 250 inci  gözlem ( 256,642,842,982,12,54,99,488,432,101) siteleri ( bunların fiziki adreslerini de belirleyici olarak yazılabilir ) bakıyoruz . x=250 y =10 olur.

f ^x(0) < n ==  bir fonksiyonun x türevi => n ^x   sayı sistemi ile tanımlanır . Bu da bilgi tanımı olur.

Farklı zamanda oluşan olayların bize ulaşması aynı anda olmuş gibi değerlendiririz. 

Gökyüzüne baktığımız zaman birisi 1 yıl  , diğeri 10 yıl önceki yıldız olabilir . 

x yerine n , y yerine x , koyarsak istatistik notasyonundan  yüksek matematik notasyonuna geçeriz  

Bütün değerlerin ( gözlemin anda toplanması ) toplamı aşağıdaki gibi yazılır .

Bir fonksiyonun Maclaurin  açılımı şeklinde yazılımı

f(x) = f(0) + x/1! f¹(0) + x² / 2! f²(0) + ...... + x ⁿ / n! f²(0) +.. + 

Gözlem fonksiyonu yazılır .

e ^x  = 1 +x/1! +x ²/2! + ... x ⁿ / n!  Doğal sayı 

Roma devrinde yüksek  matematiği ve ona bağlı fiziği anlatmak gibi  Günümüzün ilkel matematiği ( Geleceğin matematiğine göre ) ile siber uzay algısının doğa yasalarına uyarlanmasını açıklamak biraz zor . 

   Fonksiyon geometrinin  sayısal ifadesidir. 

 Permutasyon kombinezonu küçük olan değer 3  için üçlük sayı sistemi ile bilgi tanımlanarak  mekanımız yazıldı . dördüncü boyuta permutasyonu tanımladık ve 4 boyutlu eğik uzayımız ortaya çıktı .

      Örneğin = x²+y²+z²+t²= r²   uzayda yaşadığımız farz edebiliriz. Bu geometrik tanımın geometrik şekli Açık dışa büküm ise  kinetik enerji ( ısı , mekanik hareket vs ) , açık içe bükümlü  Potansiyel Enerji  ( Yerçekimi , manyetik bağlar , nükleer enerji vs ) , Kapalı  ( Kendi ekseni etrafında dönme hareketi gibi ) dışa bükümlü ise  Madde , Kapalı içe bükümlü ise anti madde . Madde yi   fonksiyon ( geometri ) olarak tanımlamış oluruz.

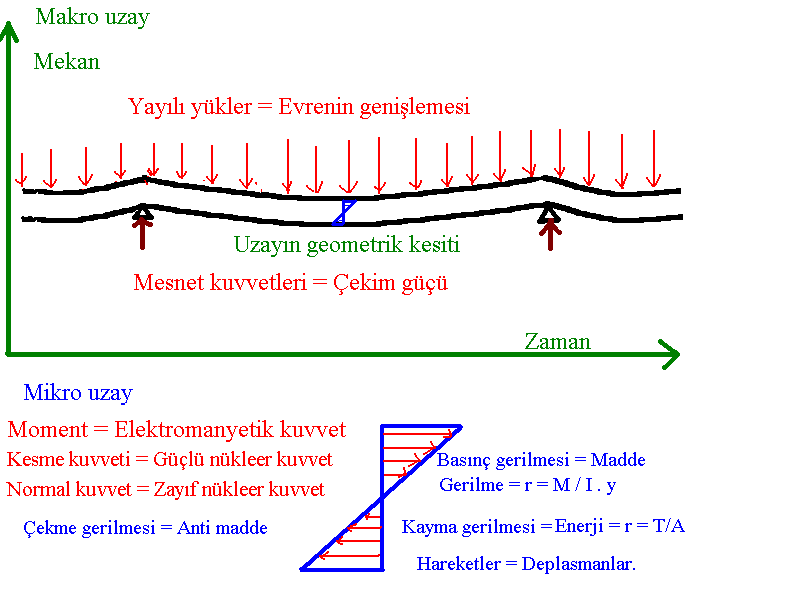
  Düz kağıdı (  kağıt yarı elastikide olabilir . ) alır kırıştırırsak iki boyutluluk özelliğini kaybetmediği halde birçok kıvrımlar oluşur . Bu kıvrımlar  madde ve Enerjidir diyebiliriz. Bu işlem esnasında oluşan kuvvetlerde statik anlamda ( deplasman evrenin genişlemesi ) yayılı yük ( Evreni genişleten kuvvet büyük patlamanın ) Mesnet kuvvetleri ( Çekim kuvveti ) Moment ( Elektromanyetik kuvvet ) Kesme kuvveti ( Güçlü nükleer kuvvet )  Normal kuvvet ( Zayıf nükleer kuvvet ) şeklinde doğanın dört kuvvetini açıklarız. Her şeyin teorisi , birleşik teori  mikro uzay ve makro uzayın birleştiren teori .

Eneji = Kuvvet x Yol  => Moment = Kuvvet x Kuvvet Kolu =>  Dalga  boyu  x  Frekans = mc2 

bu dalga boyunun (λ) ,kütlesine (m),hızına ve planck sabitine(h) bağlı λ = h / mv  

Einstein şu sonuca vardı: Işınım sadece belli kesikli miktarlarda yayımlanır

ve her zaman böyle kesikli paketler-ışık kuantları halinde bulunurlar. Böylece ışık kuantları

momentumu p=hl/c=h/l şeklinde ifade edilir. Buradan, hareketli bir cismin çarpma ile

meydana getirdiği mekanik etki momentumu ile aynı anlama geldiği için, ışık kuantının mekanik

etkisi=momentumu, dalga boyu küçüldükçe artar şeklinde bir yoruma ulaşılır.

Her parçacığa bir Broglie dalgası eşlik eder. E=hl=mc2 formülünden yola çıkarak eşlik

eden dalga, l=h/mc ile hesaplanabilir ve Compton dalga boyu olarak adlandırılır. Burada, E:

enerji, h: Planck sabiti, m:kütle, c: ışığın hızı, l: eşlik eden dalga boyunu temsil eder. Örneğin,

ışığın %1 hızıyla hareket eden (1.0x106 m/san) elektrona 7.3x10-10 metre ya da 7A0 genişliğinde

bir dalga eşlik eder. Açık olarak hesaplayacak olursak:

l= 6.6x10-34 Js / (9.1x10-31kg)(1.0x106m/s)= 7.3x10-10m@7Angstrom

Makroskobik cisimlerin momentumları çok daha büyük olduklarından Louis de Broglie

dalgasının dalga boyu çok küçüktür. Bu nedenle makroskobik cisimlerin dalga özellikleri atom

altı partiküllerde olduğu gibi gözlenemez. Bir parçacığın ya da cismin enerjisi (enerji eşittir

kütle ve E=hl=mc2) ne kadar yüksekse, dalganın uzunluğu da o kadar kısalır. Biraz daha kütleyi

büyütecek olursak, 75 kg ağırlığında olan insanı göz önüne alacak olursak ve bu kişi 5

metre/saniye hızında koşarsa 1.7x10-36 metre genişliğinde bir dalga gövdesine eşlik eder. İnsan

l=6.6x10-34 Js / (75kg)(5.0m/s)= 1.7x10-36m eşlik eden dalga boyu olarak elde edilir.

Elektronun dalga özelliği atom düzeyinde çok büyük olmasına karşın, makroskobik cisimlerin

dalga yapısı çok küçük olduğundan gözlenemez.

Ervin Schrödinger, Broglie’nin maddenin eşlik eden dalga ve dalga davranışı esas alarak farklı

fiziksel problemlere matematiksel olarak adapte etti. Klasik mekaniğe göre, bir parçacığın

kütlesi me ve x,y,z yerlerinde potansiyel enerjisi V(x,y,z) ise, potansiyel enerjileriyle ve kinetik

enerjileri (p2/2me) toplamı parçacığın tüm enerjisini verir: V(x,y,z)+p2/2me=Etoplam.

Ardından Schrödinger, parçacık ya da parçacıklar sisteminin farklı yerlerde ne dereceye

kadar bulunduğunu gösteren dalga fonksiyonu eşitliğini ortaya koydu. Sonradan dalga

fonksiyonunu ekleyerek farklı uzaysal yerleşimler için bir dalga fonksiyonu y(x,y,z) oluşturdu.

Böylece Schrödinger’in zamana bağımlı diferansiyel denklemi 1926’da doğdu. Bu denklem öyle

yazılmıştır ki, maddesel cismin hareketini tanımlayan fonksiyon bir dalganın bütün özelliklerini

taşır. Steven Weinberg’in deyişiyle “Bir yandan, herhangi bir sistemin dalga işlevinin zaman

içinde nasıl değiştiğini determinist bir yaklaşımla tam olarak betimleyen Schrödinger denklemi,

öte yandan, tümüyle bağımsız bir şekilde bizim ölçülerimize göre oluşmuş, kabul edilebilir farklı

sonuçların olasılıklarını hesaplamak için dalga işlevinin nasıl kullanılacağını bize bildiren bir

ilkeler bütünü” ortaya çıktı. Daha sonra bu denklem KM’inin yaygın kabul edilen formülü oldu.

Bir kuantum sisteminde ölçüm-gözlem yapılmadığı sürece, Schrödinger denklemi geçerlidir.

Denklem basit görünüşü ile Dirac parantezlerini de (bra| ve ketñ kullanılarak, |xñ gibi) içerecek

şekilde yazıldığında:

h şeklinde ifade edilebilir.

Burada, |yñ üzerine işlem yapan ¶/¶t (zamana göre kısmı türev) |ψñ’nin zamanla değişim

miktarını verir. H, Hamilton fonksiyonudur. Hamilton fonksiyonu, sistemdeki tüm fiziksel

nesnelerin hepsinin konum koordinatlarını qi ve momentum koordinatlarını pi cinsinden yazılan

toplam enerji ifadesidir. Bu denklem çizgiseldir. Yani, |ψñ ve |jñ denklemi sağlıyorsa, |ψñ+|jñ’de

sağlar. İki olası alternatif durumun çizgisel birleştirimi, U (Unitary) ile ayrıştırılamaz. Sonuçta

bir seçeneğin ayakta kalması için, ayrı bir yöntem olan R’ye gereksinim vardır.

Denklemin daha karmaşık bir diğer gösterimi ise;

( ; ) 2

i y y + y

h ¶ h şeklindedir.

Non-relativistik zamana bağımlı Schrödinger denkleminde, D (delta) operatörü bir

boyutta D = ¶ / ¶c ve üç boyutlu uzayda D = (¶ / ¶c) + (¶ / ¶y) + (¶ / ¶z) serbest

parçacıklar için; y f

y - =

Ñ - 2

2 4 ( ) 8

şeklinde yazılabilir. Atoma bağlı

elektronlar veya başka bağımlı parçacıklar içinse; y f

Ñ y + 8 ( - ) =

2 E U

Burada, Ñ2 Laplace operatörü olarak tanımlanır (veya D ) ve bu

Ñ2=(¶2/¶x2)+(¶2/¶y2)+(¶2/¶z2) durumuna eşittir. V(x,y,z)’deki, M kütleli

parçacı(klara)ğa uygulanan kuvvetlerin yarattığı potansiyel enerji (U ya da V), y zaman ve üç

boyutlu (x,y,z) koordinat fonksiyonu, i= -1 , ħ ise Planck sabiti (6.626076*10-34 Joule saniye)

olan h’in 2p’e bölünmesinden elde edilir. Bu formülle fizikçiler atom dünyasının akıl almaz

uyumlu tasvirini geliştirilmiştir ve sadece özel problemlere uygulanan bir denklem değildir.

Elektron Nötrinosu νe >0,00001 0

Muon Nötrinosu νμ Bilinmiyor 0

Muon μ- 106,6 -1

Tau Nötrinosu ντ Bilinmiyor 0

Tau τ- 1784 -1

             Bir elektron hız, kütle , elektrik yükü , hareket yönü dört  pencere ( iletişim kanal sayısı ) kullanır . Gözlenir değişim sayısı da çok sınırlıdır . Bir hücre için 30 ise bir Memeli havan için etkili iletişim kanalı doğada yetiştirilmiş ise 300 olarak gösterile bilinir. 

      Renk kavramı doğaya ekstra boyut kazandırır .  Eski Yunanlılar 3 buut dışında dünya algısına sahip olamadıkları için renkleri göremezlerdi . Az gelişmiş toplumlarda renk , sayı , kelime algısı parmakla sayılacak kadar azdır . Eğitimle birlikte ( Oku ! = Algıla !) algı kanalları (iletişim kanaları ) artar . Çünkü fonksiyonun   tanımlanabilirlik alanı geniştir . 8 haneli hesap makinesi ile 12 hanelik sayı gerektiren işlemi yeterli doğrulukla yapamazsın !

Uzayda ilginç deney!

  NASA’NIN Endeavour mekiğiyle Uluslararası Uzay İstasyonuna giden Japon astronot Takao Doi, burada yaptığı deneylerde bumerangın uzayda da geri geldiğini keşfetti. Doi’nin yerçekimsiz ortamda fırlattığı 3 kollu bumerang kendi ekseni etrafında dönerek geri döndü. Bu deneyi yapmasını bumerang dünya şampiyonu vatandaşı istemişti.

   Hiçbir cisim  havasız ortamda geri dönemez . Momentum korunumu yasası gereği , bumerang  uzay aracını dışına firlatılırsa , sonsuza kadar aynı doğrultuda yoluna devam eder. Momentum korunumu çekim kuvvetni kullanarak aşılması mümkün olabilir . Bu yapılabilirse ışık hızı aşılabılır . Işık hızının aşılması yaşadığımız evrenin paralel uzaya dönüşmesi demektir ki bunun anlamı ; teknolojik olarak , evrenin en uzak noktasına çok kısa zamanda seyahat mümkün olur.

    Matematikçi  doğayı okur , Fizikçi doğayı yazar . 

   Hazretti  Muhammet okudu ve yazdırdı !

       bir